

Geometrically, it is perpendicular to the level curves or surfaces and represents the direction of most rapid change of the function. When you compute df /dt for f(t)Cekt, you get Ckekt because C and k are constants. It is a vector field, so it allows us to use vector techniques to study functions of several variables. 11 Partial derivatives and multivariable chain rule 11.1 Basic dentions and the Increment Theorem One thing I would like to point out is that you’ve been taking partial derivatives all your calculus-life. The gradient is one of the key concepts in multivariable calculus.

Hint: Use the chain rule and the identity det(AB) det.
Chain rule calculus multivariable how to#
So for a general proof, one should first understand little-o notation as in the other answers. Ive got a question on how to achieve this proof correctly (2nd year vector calculus) : Assuming that u u (r, s), v v (r, s), r r (x, y) and s s (x, y) are C1 functions, prove that (u, v) (r, s) (r, s) (x, y) (u, v) (x, y).
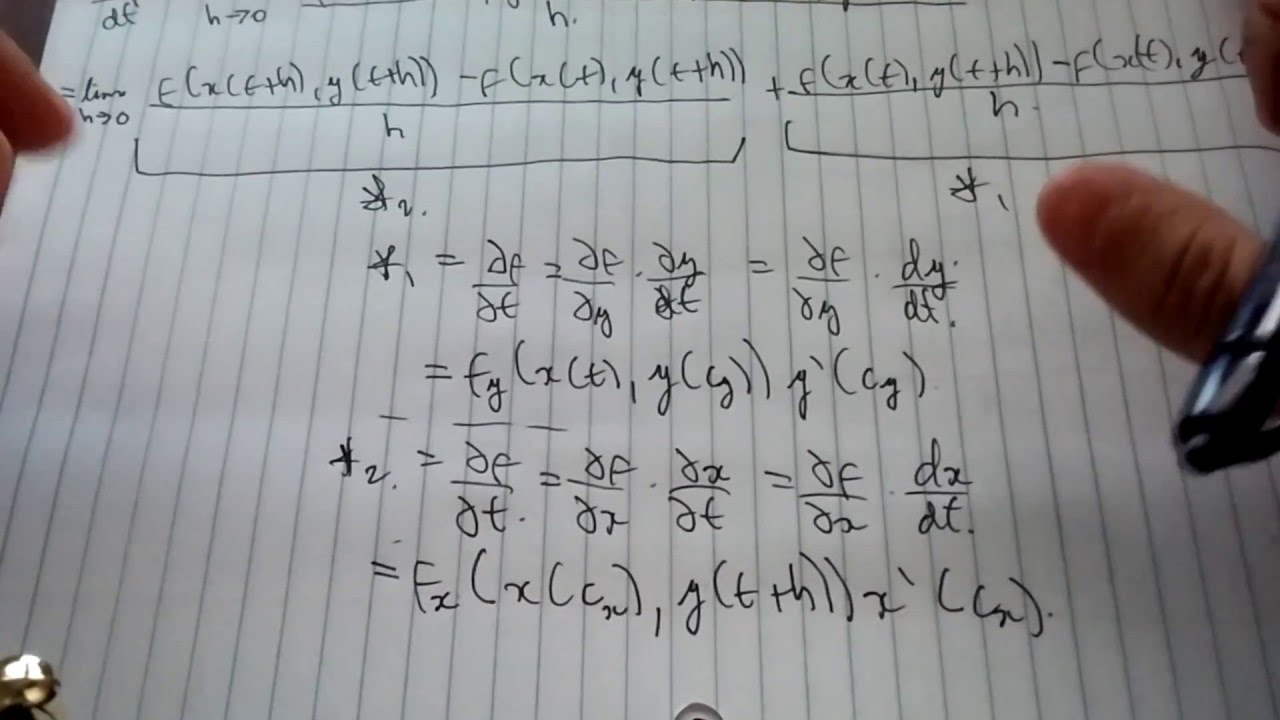
The version with several variables is more complicated and we will use the tangent approximation and total differentials to help understand and organize it.Īlso related to the tangent approximation formula is the gradient of a function. Yet, the multivariable chain rule works for the function being just differentiable at that point. Partial Derivatives Part B: Chain Rule, Gradient and Directional DerivativesĪs in single variable calculus, there is a multivariable chain rule.


 0 kommentar(er)
0 kommentar(er)
